パチスロシミュレートをpythonで行ったら組み合わせ爆発した件

概要

パチスロを遊ぶにあたって重要なことはいくつもあるが、設定判別を行うのも重要なことの一つである。
例えば1000ゲーム回した時に設定差のある部分を確認し、今打っている台の設定を推定することがある。

しかし基本的には1000ゲーム時点で上位の設定と推測できる場合でも3000ゲーム到達時には下位の設定になっている場合もあり、一日中打った場合(大体8000~10000G)でも設定通りにならない場合もある。

そこで設定毎に、あるゲーム数を回した時に設定差のある部分が出現した回数毎に確率を求めてみる。例えば、1000ゲーム回した時の出現率に設定差のある小役が10回出たときに、この事象がおきる確率が各設定でどれだけあるのかを見てみることとなる。

しかしこの計算時に組み合わせ爆発が起きたのであった…

定式化してみる

ゲーム数を、小役出現確率を、出現回数をとおく。するとゲームで出現確率の小役が回出現する確率は二項分布に従う。よって
\begin{eqnarray}
P_{n,p}(m) = {}_nC_m p^m (1-p)^{n-m} \label{eq1}
\end{eqnarray}
となる。ここのは、、だとpythonでは以下のように計算できる。

from scipy.special import comb
comb(10,3)
# 120.0

問題点

しかしここからが問題。が少ないなら問題ないが、、とすると簡単にinf、つまり無限と表示される。つまりは組み合わせ爆発が起こり、pythonの桁数表示の限界に達する。こうなるとが十分に小さくてもの計算結果は無限になってしまう。

対策案1 ~数列的に解いてみる

まずはを数列的に考えてみる。実際に計算すると、
\begin{equation}
P_{n,p}(m+1) =\frac{p(n-m)}{(1-p)(m+1)} P_{n,p}(m) \label{eq2}
\end{equation}
となることがわかる。あとはを計算して、後は上の計算式にそって計算しておけば組み合わせ爆発による無限に発散するようなことはなくなる。

これで問題解決ですね～なんて思ってたら問題が発生。計算式の一部であるを、、の場合に計算してみると、

(1 - 1/13.5)**(10000-1)
# 0

となる。計算結果があまりにも小さすぎて0になってしまうのだ。これで数列として計算してもの場合はすべて0になってしまう。が非常に小さい場合、つまりが十分1に近い場合は大丈夫かもしれないが、おそらく一番設定差としてみたい部分はせいぜい ~ 程度なので使えない。

対策案2 ~対数をとって計算してをとる

計算の順番を変更するなどして対策を試みたが断念。思いついた中で一番現実的な方法は、対数をとって計算して、最後の結果のをとる。対数をとれば大概の値は桁数限界に達することはないだろう。まずはよりの場合を計算すると
\begin{align}
\log P_{n,p}(1) &= \log {}_nC_1 p^1 (1-p)^{n-1}\nonumber\\
&= \log np(1-p)^{n-1}\nonumber\\
&= \log n + \log p + (n-1)\log (1-p) \label{eq3}
\end{align}
となる。またに対して対数を計算すると
\begin{align}
\log P_{n,p}(m+1) &=\log \left( \frac{p(n-m)}{(1-p)(m+1)} P_{n,p}(m) \right)\nonumber\\\
&= \log p + \log (n-m) - \log(1-p) - \log(m+1) + log P_{n,p}(m) \label{eq4}
\end{align}
となる。とを使うと計算することが任意のに対してを計算することができる。あとは対数をもとに戻せばいいので、を計算すればよい。実際にpythonで書くと以下のような感じ。とりあえずどういう風に確率が変化するのかプロットするところまでやってみる。

%matplotlib inline
import pandas as pd
import numpy as np

n = 10000
p = 1/13.5

piL = np.log(n) + np.log(p) + (n-1) * np.log(1-p)
pLs = [piL]

for i in range(2, n):
    piL += np.log(p) + np.log(n-i) - np.log(1-p) - np.log(i+1)
    pLs.append(piL)

pd.DataFrame({"p":pLs}).assign(p = lambda df: np.e ** df["p"]).plot()

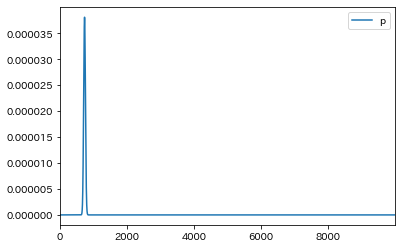
横軸がゲーム中出現した小役数、縦軸がその時の確率を表す。

対策案3 ~一番スマートな方法

最初に言った通り今回は二項分布を考えているので、専用パッケージを使って確率密度関数から計算するのが一番簡単。使うのはscipy。

%matplotlib inline
import pandas as pd
from scipy.stats import binom
n=10000
p = 1/13.5

k = np.arange(n+1)
pd.DataFrame({"A":binom.pmf(k, n, p)}).plot()

実際に全設定の確率を可視化してみる

今回はバーサスのベル出現確率を対象に計算してみる。具体的な計算はscipyを使う。

import pandas as pd
from scipy.stats import binom
n=10000 #トータルゲーム数

df = pd.DataFrame({"n":[i for i in range(1, n+1)]})

prob = {"1":1/13.5, "2":1/13.2, "5":1/12.9, "6":1/12.5} #出現確率
for i in prob.keys():
    k = np.arange(n)
    df = df.assign(s = binom.pmf(k, n, prob[i])).rename(columns={"s":"s"+str(i)})

df.set_index("n").assign(ss=lambda df: df.sum(axis=1)).pipe( #nをindexにして行ごとの和を列に追加
    lambda df: df[df["ss"] > 0] #合計が0よりも大きいところに絞り込み
).reset_index().set_index( #indexをリセット
    ["n", "ss"] #nとssをindexにセット
).stack().reset_index().rename(columns={0:"p"}).assign( #縦積みして列名を変更
    p = lambda df: df["p"] / df["ss"] #各出現回数による確率を割合に変更
).set_index(["n", "level_2"]).drop("ss", axis=1).unstack().pipe( #nとlevel_2をインデックスにセットしてss列を除去、横展開
    lambda df: df[df[("p", "s1")] > 0.01] #設定1の比率が0.01より大きいところに絞り込み
).pipe(
    lambda df: df[df[("p", "s6")] > 0.01] #設定6の比率が0.01より大きいところに絞り込み
).plot.area()

横軸が小役の出現回数、縦軸が出現回数に応じて設定別に起こる確率の比率を表す。青が設定1、オレンジが設定2、緑が設定5、赤が設定6。つまり赤の領域が広いところが設定6の確率が大きいことがわかる。ほぼ中間地点であるベルの出現回数が770回のところはに当たるので、10000ゲーム回したところだとどの設定もほぼ均等の確率であり得ることになる。 逆に800回ベルが出現していればほぼ設定5以上となることがわかり、別の偶奇判定を使えば5か6どちらかの判断ができる。

終わりに

今回は二項分布を相手にしたことで組み合わせ爆発がおきてしまった。今回は数列的に計算し、さらに対数をとることで非常に大きな数値に対しても計算可能であることが確かめられた。
とはいえそれでも面倒なのでscipyを使うのが一番簡単な方法だろう。
…対数とった方法で実装して満足した後、湯船の中でscipyを使うことを思いついたのは内緒の方向で。